3d~def User's Manual

Introduction

Warning - this manual assumes that you understand the basics of elastic deformation theory and the ideas that underlie boundary element algorithms! This manual contains all the nitty-gritty nerdy stuff about setting up input files with the appropriate boundary conditions, formats, etc., how to make the program run, and what sort of output it can generate.
We have attempted to make this program platform independent and operable on any basic computer (only a Fortran compiler is required). This made our job easy, as you have to provide all the graphics. The codes are written in generic Fortran and no structures are used. The code does contain some internal comments for those brave enough to look into it.

Table of Contents

I. Program structure.

II. Definitions and conventions.
A. Green's functions.
B. Selected definitions.
C. Boundary condition codes.
D. Background deformation specification.
E. Displacement direction, sign, and fault geometry conventions.
F. Units.
G. Tensor notation.
 
III. Input file description.

A. Introduction to the input file.
B. Input file (material properties, element geometry, boundary conditions).
C. Input file (output control).
IV. Output file descriptions.
A. Column output format.
B. Vector output format.
V. Acknowledgements.

 

I. Program structure

Four files contain source code (Fortran text):

3D_MAIN.F, OKADA_SUB.F, XYZ_OUTPUT.F, VECTOR_OUTPUT.F

In order to compile the source code two include files are required. These are:

SIZES.INC, UNITS.INC

(Include files contain Fortran statements that are inserted into the source code automatically upon compilation. They simplify making changes to the program; for example, to change the maximum number of allowable elements (see Section II.B) one would only modify a single parameter specified in the file SIZES.INC. All appropriate array dimensions within the four source code files would then be changed appropriately without having to edit them.)
SIZES.INC contains program dimensions that depend on the number of elements. The largest array (computer memory accessed as an indexed matrix) has dimensions of (MAX3_ELEM)*(MAX3_ELEM+1) where MAX3_ELEM=3*MAX_ELEM and MAX_ELEM is the maximum number of elements allowed. You should make this number as large as you will need for your specific problem by editing the file SIZES.INC before compiling the program. If the program does not run and the computer returns an 'insufficient memory' error, you will have to reduce this number. The memory useage could be made much more efficient if dynamic memory allocation was implemented - this wasn't available for Fortran at the time the program was written, and we haven't gotten around to updating it.
UNITS.INC contains all file unit numbers ('tags' used by the computer to identify a file when reading or writing to it). You can change these as needed and re-compile the source codes to implement the changes.

The basic parameter specification (input) is done in the code contained in the file 3D_MAIN.F. All major calculations are done in routines contained in files 3D_MAIN.F and OKADA_SUB.F. Routines that control the output grid and information written to column formatted files are contained in the file XYZ_OUTPUT.F. Each row of these output files contains the X,Y,Z coordinates of each grid point and specified calculated quantities. These column formatted output files are read by routines in the file OUTPUT_VECTOR.F and the information they contain is reformatted in a vector format (as required by many plotting programs such as MATLAB, IDL, etc.). Vector reformatting is optional.

The program does not generate any graphical output - displaying the output is left up to you.


Return to Table of Contents


II. Definitions and conventions

A. Green's functions.
3D-DEF uses Green's functions calculated using subroutines provided by Y. Okada. The Green's functions relate the deformation field (displacements and displacement gradients) to a rectangular dislocation in a homogeneous half-space (a semi-infinite medium bounded by a planar free-surface). Descriptions of the dislocation theory underlying the routines may be found in Okada, Y., Internal deformation due to shear and tensile faults in a half-space, Bull. Seismo. Soc. Amer., v. 82, 1018-1040, 1992.

Return to Table of Contents

 

B. Selected definitions.
The meaning of an element and the coordinate systems used in the computational algorithms are defined in this section. Three coordinate systems are used. A local coordinate system is defined for each element because the Green's functions (see Section II.A) are most efficiently calculated in the local coordinate system of the element. An in-plane coordinate system is also defined for each element because the boundary conditions are specified either on or orthogonal to the element surface. A global coordinate system is required so that the effect of the deformation field associated with one element on another element can be calculated. Because the parameters describing the deformation are calculated in local coordinates, they must be transformed into a global system that is common to all elements.

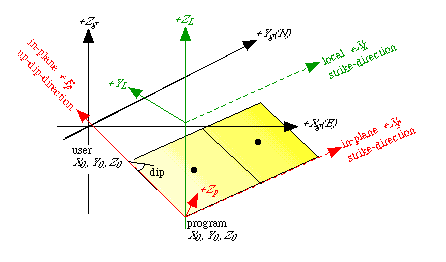
Figure 1

Return to Table of Contents


C. Boundary condition codes.
The boundary condition codes define the constraints on each sub-element, one boundary condition for each directional (strike, dip, normal) component of stress or displacement. Boundary conditions may include the magnitude of the directional components of stress, of absolute displacements, or of relative displacements on a sub-element. For a single sub-element, mixed (stress and displacement) boundary conditions may be specified.
The stresses are continuous everywhere and displacements are discontinuous across elements. Understanding the difference between absolute  and relative  displacements is very important when specifying boundary conditions and interpreting the program output. Once you understand the difference, you are well on your way to mastery of boundary element modeling! The program calculates (solves for) relative  displacement on all of the sub-elements in the model such that the strain energy within the half-space is a global minimum. Relative  displacement is simply the net dislocation or slip of one side of the element with respect to the other side  (for example, the fault offset observed after an earthquake). The relative displacements solved for by the program (that minimize the strain energy) are determined by the user specified boundary conditions on the sub-elements. The relative displacement on a particular sub-element or group of elements may also be specified by the user, rather than being treated as an unknown. Absolute  displacement refers to the motion of the footwall side of the element with respect to the global coordinates (HOWEVER: the displacements are specified in the planar coordinates of the sub-element; that is: strike direction, dip direction, fault-normal direction). Mathematically, the relative displacement is the difference between the absolute displacements of either side of the element. For example, the normal component of relative displacement, Dn, is

Dn = un- - un+

where un- is the magnitude of the motion of the footwall (absolute displacement) in the direction normal to the element and is un+ is the absolute displacement of the hanging wall.

The user specifies one boundary condition code (a number) for each sub-element. Each code actually constrains the magnitude of three parameters (stresses or displacements) at the center of the sub-element, one in the strike direction, one in the dip direction, and one in the direction normal to the sub-element surface. The boundary condition codes allowed are:

Code#....Direction in the Plane of the Sub-element...............................................
...........strike (shear)....................dip (shear).......................normal (tensile)

1 ........ absolute displacement......absolute displacement......absolute displacement
2 ........ stress...............................stress................................stress
3 ........ stress...............................absolute displacement......stress
4 ........ absolute displacement.....stress................................stress
5 ........ stress...............................stress...............................absolute displacement
10 ...... relative displacement.......relative displacement.......relative displacement
11 ...... angle (degrees)................stress (at specified angle).relative displacement
12 ...... stress...............................stress...............................relative displacement
13 ...... stress...............................relative displacement.......relative displacement
14 ...... relative displacement.......stress...............................relative displacement

Note that Code #11 and Code #12 specify the same stress conditions; for Code #11 the user specifies the direction of shear as an angle measured from the strike direction, which is then resolved into shear stress conditions in the strike and dip directions.

Return to Table of Contents

 

D. Background deformation specification.
It is possible to include a uniform deformation field, referred to as a background deformation field. (For example, suppose one wanted to investigate how slip was partitioned among a network of faults driven by a uniform simple-shear strain field.) The field is specified as a stress, strain, or displacement gradient tensor. Internally these tensors are converted to a stress tensor and a rigid body rotation (if a displacement gradient tensor is specified). The background stresses are subtracted from the stress boundary conditions before solving for the relative displacements on the sub-elements. Because the background deformation is added to that associated with the sub-element displacements, the resultant stresses on the sub-elements are thus guaranteed to equal the boundary condition stress value. Use of a background stress or strain tensor will have no affect on the sub-element relative displacements if you use Codes 1 or 10 because the boundary conditions do not involve stress. If a displacement gradient tensor is specified, then the only affect will be to modify the output displacements by any rigid body rotations associated with the background displacement gradient field.
Section III.B explains how to specify the input to include (or not include) a uniform background deformation field.

Return to Table of Contents

 
E. Displacement direction, sign, and fault geometry conventions.
The orientation of each fault (element) is specified as follows:
Fault (element) relative displacement sign conventions are:
Dislocation Component ..................Sign...................... Faulting Mode
Strike ..............................................>0 (positive).......... left-lateral
........................................................<0 (negative)..........right-lateral
Dip .................................................>0 (positive) ......... thrust
........................................................<0 (negative) .........normal
Tensile (normal to plane) ............... >0 (positive) ........ opening
........................................................<0 (negative) ....... .closing
 
COMPRESSIVE stresses are NEGATIVE and yield an EXTENSION that is POSITIVE. I.e. sigma 1 is negative, X (strain) is positive.

Return to Table of Contents

 

F. Units.
Specify input element (fault) dimensions in kilometers and displacements in centimeters. Output displacements have units of centimeters, strains are dimensionless. Stresses (input and output) have the same units as the Young's modulus specified in the input file.

G. Tensor notation.
Stress tensors are written as a vector internally as:
Vector Index Stress Component

1 Sxx
2 Sxy
3 Sxz
4 Syy
5 Syz
6 Szz

 

x,y,z refers to whatever coordinate system is being used at the time the values are examined (for example, directly out of the subroutines that calculate the Green's functions x,y,z refers to the local XL,YL,ZL coordinate axes). Strain tensors are also written in the same manner.

Return to Table of Contents

 

III. Input file description.

A. Introduction to the input file.
The program requires one input file and the amount of interactive input is variable depending on what options the user selects. All input parameters may be written to a file so that the only interactive step is to respond to the program prompt for the input file name. Alternatively, the user can interactively enter the type and characteristics of the information written to output files.
All lines in the input file containing numbers are free formatted so the format is not important but items cannot be omitted. Text lines that begin with an asterisk are provided only for the user's benefit and are ignored by the program. Note that while you can write anything in these lines, the number of asterisk lines and blank lines must not change.
The first part of the input file contains parameters that describe the material properties of the medium, the element geometry, and the boundary conditions. The second part of the file controls which properties of the deformation field are calculated and output and where within the half space (and in what coordinate system) these properties are calculated. This second part of the file may be omitted and the needed input entered interactively.

Return to Table of Contents

 

B. First part of the input file (material properties, element geometry, boundary conditions).
An example and explanation of the first part of an input file is now provided. The text below refers to Manual Example A. The first line of the input file must begin with an '*' and can contain any comments thereafter; here the comments describe what the line following contains. The second line contains 5 fields; the first four are numbers, and the last is a character string. The numbers are (from left to right) the Poisson's ratio (dimensionless), the Youngs modulus (units of your choice), the number of elements or planes in the model, and the coefficient of internal friction. The coefficient of internal friction is used to determine potential failure planes, assuming a Coulomb failure criterion; if you don't select the 'failure plane' output (see Section IV) this coefficient has no influence on the results. The final item in this line is a character string flag set to specify the type of background deformation field that will be specified; the character string should be 'none' for no background deformation field, 'stress' for a background stress field, 'strain' for a background strain field, or 'displacement gradient' for a background displacement gradient field. The next line is blank if the above flag is 'none' or contains the elements of the background deformation tensor. The order of stress or strain tensor components is xx, xy, xz, yy, yz, zz where x,y,z refer to the global coordinate axes. For a flag set to 'displacement' the order of displacement gradient tensor components is dUx/dx, dUx/dy, dUx/dz, dUy/dx, dUy/dy, dUy/dz, dUz/dx, dUz/dy, dUz/dz.
 
A blank line and two comment lines are then followed by the next group of numbers that describe each plane, one line per plane. The first three numbers are the user reference point of the plane in global coordinates (see Section 2B). The fourth and fifth numbers describe the dimensions of the plane; the length (in the strike direction) and width (dip direction). The sixth and seventh numbers describe how the plane is sub-divided into sub-elements in the strike and dip directions. Sub-elements of a single plane all have the same dimensions; their individual length equals the plane length divided by the sixth number (under #SUB-ELEMS:STK in the sample file) and their width equals the plane width divided by the seventh number (under DIP). The last two numbers are the strike and dip of the plane in decimal degrees (see Section 2D). In this sample file two planes are specified, the first is divided into six sub-elements (three along strike and two down dip) and the second into two sub-elements.

The next group of numbers (following a blank and three comment lines) specify the boundary conditions for each sub-element, one row per sub-element. Figure 2 below illustrates how the sub-elements are identified. The first two integers are sub-element indices but are not actually used by the program; they simply help the user keep track of the sub-elements. The first sub-element must be the one at the internal reference point or equivalently, the origin of the in-plane coordinate system (looking at the plane from the hanging wall the first sub-element is in the lower (deepest) left corner). The element dip index is the second number of the pair (right index) and the values increase up-dip. The first number of the pair is the strike index and these increase with distance from the origin. For each strike index, the dip index is incremented . Diagramatically the indices of the sub-elements of the first plane in the sample file are:

 

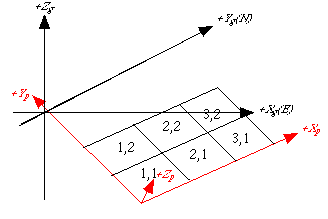
Figure 2

Return to Table of Contents

 

C. The second part of the input file (output control).
The second part of the input file may be viewed as having 5 "blocks" of input, the total number of lines in each block is determined by input in previous blocks. As a result, this part of the input file may change dramatically from model to model. Please continue to refer to Manual Example A. For examples of other types of output, see the list of addtional examples following this explanation. The first (non-comment) line of the first block (#1) determines whether the output parameters will be specified interactively or non-interactively. If interactively, nothing else in the file matters--the user is prompted from standard output for the parameters. If non-interactively is selected, this block contains two more lines. (NOTE: as will be explained in more detail below, greater control over the number and content of created files may be achieved via the interactive specification of output control.)
The line following the interactive/non-interactive choice determines the gridding of the solution; that is, whether the desired output parameters describing the deformation field are calculated at:
i) points on a plane (of any orientation)
ii) points within a volume (with vertical and horizontal sides), or
iii) a list of user-specified points.

If output of parameters describing the deformation on a plane is desired, the line must start with the character string "plane". For a gridded volume, the line must start with "vol". (For a gridded volume, all output parameters, except element relative displacements, will be in global coordinates, no matter what you write in the appropriate line). For output at a set of user-specified points, the line starts with "user". In almost all cases, only the first letter of the line is read by the program.
The next line determines the type of output, "XYZ" or "vector". For XYZ (column) output, the output files of deformation parameters contain one line per point, with the X, Y, and Z coordinates of the point given one on each line. For vector output, the values within the gridded region (which may be either a plane or a volume) are output into a file as an array of numbers, without coordinates. The coordinates of each point are determined by their position within the array (Seem Obscure? Patience, Grasshopper! Enlightenment may be obtained by reading more about this issue below in the following examples!). NOTE: if vector output is requested, both column output files and vector output files are created because the column output files are always created, and the program generates the vector files from the column output files.

The next block (#2) determines the coordinate system for calculating various parameters describing the deformation field. The two choices of coordinate systems are "global" or "in-plane"; the latter is specified with anything that doesn't start with a 'g' or 'G' (in-plane, planar, etc.). This option only applies to output on a gridded plane and affects only output stresses, strains, displacements, and gradients of displacements. Global output coordinates means that stresses, strains, displacements, and gradients of displacement are coordinate stresses, strains, etc. in the same reference frame in which the faults were specified (that is, Sxx, Sxy, Sxz, etc.). In-plane (or planar) coordinates refer to the gridded plane, that is: the output stresses, strains will be referred to the strike, dip, and normal direction of the gridded plane (that is, Sss, Ssd, Ssn, etc).

The next block (#3) determines which parameters describing the deformation field to calculate. The choices are: element displacements (that is, one side relative to the other of each element), and at each grid or user specified point, absolute displacements, gradients of displacements, strains, stresses, strain invariants, strain orientations, rigid body rotations, and failure plane orientations. These are described in detail in Section IV. The list of files containing various characteristics of the calculated deformation field can be in any order. The word on each line sets an appropriate flag so that an output file containing the parameters described by the word is generated. The program only interprets the first letter (the first 4 letters for 'stress' and 'strain') so there is some flexibility in what words are used. For example, you must write 'gradients of displacement' (if fact, simply 'g' will do) to generate an output file containing the components of the displacement gradient tensor; use of 'displacement gradients' would be incorrect and (because the key word starts with a 'd' instead of a 'g') result in an output file containing displacements.

The next block (#4) is a line containing the suffix that will be appended to the output files.

The final block (#5) specifies the points at which output is calculated. If a user array was specified in block #1, then this portion contains the number of points, and their coordinates (see example below). If a gridded plane was specified in block #1, then this section contains the orientation and size of the plane in one line, and the number of points on the plane at which to calculate the output on a second line (see example below). If a volume is specified, the first line of this block contains the coordinates of two of the corners of the rectangular prism of the volume, and the second line contains the number of X, Y, and Z grid points within the volume.

In the examples below, user input that effects the outcome of the model (that is, which output files are created, what they are called, where the values are calculated, etc.) is shown in bold. The minimum input required to obtain the desired result is underlined. Everything else in the second part of the file is ignored by the program, but is included to make the input file more intelligible to the user.
(NOTE: lines that begin with '*' must be in the input file because they are used by the program to separate blocks of differing types of input. However, they may contain any text following the '*'. )

Additional Examples:
Note that the first part of all the example files is identical to that of Manual Example A.
For a non-interactive run with a gridded plane see Manual Example B.
For a non-interactive run on a user-specified array of points see Manual Example C
For an interactive run see Manual Example D. You will then be asked by the program to answer a sequence of questions that provide the program with the required input parameters.
Return to Table of Contents
 

IV. Output file descriptions

A. Column output format.
Nine output files are created with column format. Each one has a similar format. The suffix ??? in the following discussion is replaced with the suffix that you specified in the input file (or answered interactively). Each line contains an observation point x,y,z (in global coordinates) and the parameters describing the various characteristics of the deformation field at that point. The file names and their contents are:

stressten.??? Six independent elements of the stress tensor, in the order: Sxx, Sxy, Sxz, Syy, Syz, Szz, the maximum shear stress (tmax) on an inspection plane, the rake angle of tmax, and the components of tmax in the strike and dip directions. If output on a plane is requested and global output is not requested, then these correspond to the in-plane coordinates. (For example, Sss, Ssd, Ssn, Sdd, Sdn, Snn where 's' refers to the strike direction, 'd' to the dip direction, and 'n' to the normal direction. Thus, Szz is really Snn and corresponds to the stress that is normal (tensile) to the fault plane, Sxz corresponds to Ssn and is the shear stress (sometimes called a traction) in the strike direction.) Otherwise the tensor components are referred to the global coordinate system. The maximum shear stress is a useful set of results since the distribution of tmax can be compared to the slip direction. In stress inversion techniques, these two directions are assumed to be the same.
 
strainten.??? Six independent elements of the strain tensor, Exx, Exy, Exz, Eyy, Eyz, Ezz, and the volumetric strain (Exx+Eyy+Ezz, independent of the coordinate system). If output on a plane in in-plane coordinates is requested, then these values may be output in the in-plane coordinates (as described in stressten.???).
 
displacements.??? Displacements, Ux, Uy, Uz, in the x,y,z directions, respectively. If output on a plane in in-plane coordinates is requested, then these values may be output in in-plane coordinates; Ux is in the strike direction, Uy in the up-dip direction, Uz normal to the plane.
 
dgten.??? Displacement gradient tensor, dUx/dx, dUx/dy, dUx/dz, dUy/dx, dUy/dy, dUy/dz, dUz/dx, dUz/dy, dUz/dz. As for the above, these may correspond to the in-plane coordinates if the user has selected the plane and in-plane (not global) options.
 
strainorient.??? Principal strains, and their plunge and trend with respect to the global axes. The values corresponding to the maximum principal strain are output first, and the minimum principal strain values are output last.
 
invariants.??? Strain & stress invariants including the volume change, failure stresses, octahedral shear stress, and strain energy density.
 
rbr.??? Rotations about the global x, y, and z axes.
 
failure.??? For each of the two optimal failure planes, the strike and dip of the plane and the direction cosines of the slip vector are given. The strike is clockwise from north, the dip is from the horizontal, and the direction cosines are with respect to X(E), Y(N), Z(up).
 
elements.??? Each line of the output file will contain the coordinates of the center of the element in global coordinates or in in-plane coordinates, and the relative displacements in the strike, dip, and tensile (normal) directions.

Programmer notes:
The first eight files are opened in a subroutine named 'open_opts', closed in a subroutine named 'close_opts', and written to in the subroutine named 'XYZ_Results'. The file "elements.???", is opened and closed in subroutine 'final_write' and written to in 'XYZ_elements'.

The first eight output files may be re-formatted in a vector format (that is, as desired by plotting programs such as MATLAB, IDL, etc.); this re-formatting is of course optional. Remember that if you change the format of these column formatted files, you must also change the routines in OUTPUT_VECTOR.f since they must read these files. The element displacements may also be written out in vector format but this is independent of the column formatted file.

Return to Table of Contents

 

B. Vector output format
If the user requests vector output, then the deformation output parameters will be re-written in vector format (in new files). Each parameter will be written to its own file. If the program is being run non-interactively, then all parameters of a particular selected type will be written out. For example, if the user has specified 'gradients of displacement' in the input file, nine output files will be generated - one for each element of the displacement gradient tensor. If running in an interactive mode, the user can select which parameters to be written out (that is, only the dUx/dz, dUy/dz, dUz/dz components of the displacement gradient tensor--or whatever subset is desired). See the description of the column formatted files to find out what coordinate systems may be used for the output parameters. Note that for in-plane coordinates, x is the strike direction, y is the dip direction, and z is normal to the plane. For a gridded plane, each line of the output file corresponds to a row (constant depth) on the plane; the values from left to right on each line correspond to the increasing strike direction. The first row corresponds to the shallowest depth and last row to the greatest depth on the plane or in the volume. For a gridded volume, consider the volume to be a stack of horizontal planes, the first plane is the shallowest (closest to the surface). The output is the same as for the gridded plane for each of the horizontal planes. The first value of each plane corresponds to the northwestern corner.

The following describes the output file possibilities for each output type requested, in format:
Output type
file_name.??? contents
element:
elemds#.??? strike component of displacements
elemdd#.??? dip component of displacements
elemdn#.??? tensile component of displacements
(#=index number, 1... no. of planes)
 
stress:
Sxx.??? xx component of the stress tensor
Sxy.??? xy component of the stress tensor
Sxz.??? xz component of the stress tensor
Syy.??? yy component of the stress tensor
Syz.??? yz component of the stress tensor
Szz.??? zz component of the stress tensor
tmax.??? magnitude of maximum shear stress on an inspection plane
tmx.??? x-component of maximum shear stress vector on an inspection plane
tmy.??? y-component of maximum shear stress vector on an inspection plane
The last 2 files are good for the QUIVER function inside MATLAB.
 
strain
Exx.??? xx component of the strain tensor
Exy.??? xy component of the strain tensor
Exz.??? xz component of the strain tensor
Eyy.??? yy component of the strain tensor
Eyz.??? yz component of the strain tensor
Ezz.??? zz component of the strain tensor
 
gradients in displacements
dUxdx.??? gradient of x-displacement in x-direction
dUxdy.??? gradient of x-displacement in y-direction
dUxdz.??? gradient of x-displacement in z-direction
dUydx.??? gradient of y-displacement in x-direction
dUydy.??? gradient of y-displacement in y-direction
dUydz.??? gradient of y-displacement in z-direction
dUzdx.??? gradient of z-displacement in x-direction
dUzdy.??? gradient of z-displacement in y-direction
dUzdz.??? gradient of z-displacement in z-direction
 
rigid body rotations
rbr_deg_x.??? rotation about the X (E) axis
rbr_deg_y.??? rotation about the Y (N) axis
rbr_deg_z.??? rotation about the Z (vertical) axis
 
orientation of principal axes
prince_max.??? magnitude of the max. principal strain
plunge_max.??? plunge with respect to horizontal of the max. principal strain
trend_max.??? trend (cw with respect to N) of the max. principal strain
prince_int.??? magnitude of the intermediate principal strain
plunge_int.??? plunge with respect to horizontal of the intermed. principal strain
trend_int.??? trend (cw with respect to N) of intermediate principal strain
prince_min.??? magnitude of the min. principal strain
plunge_min.??? plunge with respect to horizontal of the min. principal strain
trend_min.??? trend (cw with respect to N) of the min. principal strain
 
displacements
disp1.??? displacements in the x-direction.
disp2.??? displacements in the y-direction.
disp3.??? displacements in the z-direction.
 
invariants
delv.??? volumetric strain
aftershocks.??? failure stress
oss.??? octahedral shear stress
work.??? strain energy density
 
failure planes
strike1.??? strike of first failure plane
dip1.??? dip of first failure plane
ce1.??? slip vector dir. cos. with respect to X(E)
cn1.??? slip vector dir. cos. with respect to Y(N)
cz1.??? slip vector dir. cos. with respect to Z(up)
strike2.??? strike of second failure plane
dip2.??? dip of second failure plane
ce2.??? slip vector dir. cos. with respect to X(E)
cn2.??? slip vector dir. cos. with respect to Y(N)
cz2.??? slip vector dir. cos. with respect to Z(up)
 
element displacements - generates output on each plane, three file types are created for each -
elemds#.??? strike component of displacements
elemdd#.??? dip component of displacements
elemds#.??? tensile component of displacements

where # is the number of the plane as listed in the input file. Each contains a component of the displacement such that each line of the file corresponds to the sub-elements along strike at a fixed depth (dip index). The first line for each plane is the top (closest to the surface) of the plane and lines increment with increasing depth. A set of lines is written for each plane, and each plane is separated by a blank row.

Return to Table of Contents

 

V. Acknowledgements
The authors would like to thank P. Bodin for his input and discussions on 3D-DEF and boundary elements in general, bravery in testing the program, and assistance in writing this manual. We also thank C. Meertens and B. Anderson for being guinea pigs, and UNAVCO/UCAR and H. Benz for providing computing facilities. A. Crone and K. Haller provided extremely useful reviews of this manual.

Return to Table of Contents